Mesh accounting - Download/streaming costs
This post is the 4th in this series of posts about Blender Addons for SecondLife creation, and we (finally) get to sink our pythonic fangs into something concrete.Previously...
Post 1 - We started to put a simple addon together to generate five copies of a selected Mesh and rename them according to their intended use.Post 2 - We took it a step further by allowing the user to select which LOD to use as the source and which targets to produce.
Post 3 - We wrapped up the process, connecting the execute method of the operator to the new structures maintained from the UI.
So what next?
Tonight we are going to try (or at least start) to replicate the streaming cost calculation of SL in Blender.A quick recap
For those who have not looked lately and are perhaps a little rusty on Mesh accounting here is the summary.Firstly, I will use the term Mesh primitive to denote a single mesh object that cannot be decomposed (unlinked) in-world. It is possible to link Mesh Primitives together and to upload a multi-part mesh exported as multiple objects from a tool such as Blender.
The LI (Land Impact) of a Mesh primitive is defined as being the greater of three individual weights.
1) The streaming or download cost
2) The Physics cost
3) The server/script cost
Mathematically speaking if D is Download, P is physics and S is streaming then
LI = round(max(D,P,S))Of these S is simplest and generally speaking least significant. It represented the server side load, things like script usage and essential resources on the server. At the time of upload, this is 0.5 for any given Mesh primitive; this means that the very lowest LI that a Mesh primitive can have is 0.5, and this rounds up to 1 in-world. Because the rounding is calculated for the entire link set, two Mesh primitives of 0.5 each, can be linked to one another and still be 1LI (in fact three can because 1.5LI gets rounded down!).
Physics cost we will leave to another post, much misunderstood and often misrepresented, it is an area for future discussion.
And so that leaves Streaming cost,
If you read my PrimPerfect (also here) articles on Mesh building in the past, you will know that the streaming cost is driven by the number of triangles in each LOD and the scale of the object.
LOD, or Level Of Detail, is the term used to describe the use of multiple different models to deal with close up viewing and far away viewing. The idea being that someone looking in your direction from half a region away does not want to download the enormous mesh definition of your beautifully detailed silver cutlery. Instead, objects decay with distance from the viewer. A small item such as a knife or fork will decay to nothing quite quickly, while a larger object such as a building can reasonably be expected to be seen from across the sim. Even with a large building, the detailing of the windows, that lovely carving on the stone lintel on the front door, and so forth, are not going to be discernable so why pay the cost for them when a simpler model could be used instead? Taking both of these ideas together it is hopefully clear why scale and complexity are both significant factors in the LI calculation.
The highest LOD model is only visible from relatively close up. The Medium LOD from further away, then the low and the lowest. Because the lowest LOD can be seen from anywhere and everywhere the cost of every triangle in it is very high. If you want a highly detailed crystal vase that will be "seen" from the other side of the sim, then you can do so, but you will pay an extremely high price for it.
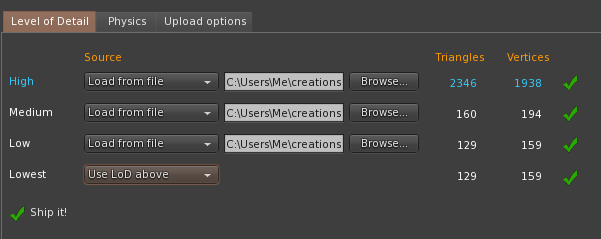
The way that most of us see the streaming cost is through the upload dialogue. Each LOD model can be loaded or generated from the next higher level. One rule is that each lower LOD level must have the same or fewer triangles than the level above it.
When I am working in Blender, I export my Mesh files, drop into the upload dialogue and see what it would cost me in LI. I then go back and tweak things, etc, etc. Far from the ideal workflow.
One of my primary goals in starting this process was to be able to replicate that stage in Blender itself. It can't be that hard now, can it?
..Sadly, nothing is ever quite as easy as it seems, as we will find out.
To get us started, we need to get a few helper functions in place to get the Blender equivalent functions.We will need to know the dimensions of the object and the triangle count of each LOD Model.
This is why we wanted a simple way to link models that are related so that we can now do calculations across the set.
def get_radius_of_object(object):
bb = object.bound_box
return (Vector(bb[6]) - Vector(bb[0])).length / 2.0
The function above is simple enough, I do not like the magic numbers (0 and 6) and if there is a more semantic way to describe them I would love to hear of it, but they represent two extreme corners of the bounding box and the vector between them is therefore 2* the radius of a sphere that would encompass the object.
def GetTrianglesSingleObject(object):
mesh = object.data
tri_count = 0
for poly in mesh.polygons:
tris_from_poly = len(poly.vertices) - 2
if tris_from_poly > 0:
tri_count += tris_from_poly
return tri_count
The function here can (as the name suggests) be used to count the triangles in any object,
At first thought, you might think that, with triangles being the base of much modelling, there would be a simple method call that returned the number of triangles, alas no. In Blender, we have triangles, and quads and ngons, A mesh is not normally reduced to triangles until the late stages of modelling (if at all) to maintain edge flow and improve the editing experience. Digital Tutor have an excellent article on why Quads are preferred.
The definitive way to do this is to convert a copy of the mesh into triangles using Blenders triangulate function, but we want this to work in realtime, and the overhead of doing this would be phenomenal. The method I settled on was a mathematical one. The Mesh data structure in Blender maintains a list of polygons. Each Polygon, in turn, has a list of vertices. We can, therefore, iterate over the polygon list and count the number of vertices in each poly. For each polygon, we need to determine the number of triangles it will decompose in to. A three-sided is a single triangle, of course, A four-sided polygon, a quad, decomposes, ideally, into two triangles, a five-sided poly gives us a minimum of three. The pattern is clear. For a polygon with N sides, the optimal number of triangles is N-2. What is less clear to me is whether there are cases that I am ignoring here. There are many types of mesh some more complex than others. If there are cases where certain types of geometry produce no conformant polygons, then this function will not get the correct answer. For now, however, we will be content with it and see how it compares to the Second Life uploader's count.
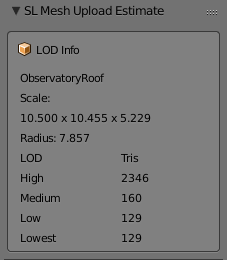
Armed with these helper functions, and the work we did previously, we can now add the counts that we need to a new Blender UI panel as follows.
So let's see if this compares well with the Second Life Mesh uploader.
Spot on. So far so good. Enough for one night, tomorrow we'll take a deeper dive into the streaming cost calculation.
Beq
x


No comments:
Post a Comment